Մեկ փոփոխականի քառակուսային ֆունկցիա

Քառակուսային ֆունկցիա, երկրորդ աստիճանի ամբողջ ռացիոնալ ֆունկցիա։ հավասարումը քառակուսային ֆունկցիա է և պարունակում է քառակուսի եռանդամ, որտեղ և ։ Քառակուսային ֆունկցիայի գրաֆիկը պարաբոլ է։ Քառակուսային ֆունկցիայի շատ հատկություններ կապված են պարաբոլի գագաթի հետ, որը որոշում է գրաֆիկի դիրքը և տեսքը։
Հիմնական հատկություններ
[խմբագրել | խմբագրել կոդը]Քառակուսային ֆունկցիայի շատ հատկություններ կախված են գործակցի արժեքից։ Հետևյալ աղյուսակը ամփոփում է քառակուսի ֆունկցիայի հիմնական հատկությունները[1]։
| Հատկություն | ||
|---|---|---|
| Ֆունկցիայի որոշման տիրույթ | ||
| Ֆունկցիայի արժեքների տիրույթ | ||
| Ֆունկցիայի զույգությունը | Զույգ է դեպքում, կենտ է դեպքում | |
| Ֆունկցիայի պարբերականությունը | Ոչ պարբերական ֆունկցիա | |
| Ֆունկցիայի անընդհատությունը | Անընդհատ է, խզման կետեր չկան | |
| Ֆունկցիայի զրոները | , եթե իրական զրոներ չկան, եթե | |
| Ֆունկցիայի սահմանը դեպքում | , դեպքում | , դեպքում |
| Ֆունկցիայի դիֆերենցելիություն | Ամենուր բազմակի դիֆերենցելի է | |
| Էքստրեմումի կետերը (բացարջակ էքստրեմում) | (մինիմում) | (մաքսիմում) |
| Խիստ մոնոտոնության միջակայքերը | նվազում է աճում է | աճում է նվազում է |
| Ֆունկցիայի ուռուցիկությունը | Ամենուրեք գոգավոր ֆունկցիա | Ամենուրեք ուռուցիկ ֆունկցիա |
| Ճկման կետ | Ճկման կետերը բցակայում են | |
| Ֆունկցիայի սահմանափակումները | Սահմանափակ ներքևից | Սահմանափակ վերևից |
| Ֆունկցիայի առավելագույն արժեքը | Բացակայում է | |
| Ֆունկցիայի նվազագույն արժեքը | Բացակայում է | |
| Ֆունկցիայի դրական արժեքները | ||
| Ֆունկցիայի բացասական արժեքները | ||
Գործակիցների ազդեցությունը գրաֆիկի ձևափոխության վրա
[խմբագրել | խմբագրել կոդը]Քառակուսյին ֆունկցիայի գրառման ստանդարտ ձև
[խմբագրել | խմբագրել կոդը], и իրական թվերը քառակուսի ֆունկցիայի ընդհանուր արձանագրման մեջ կոչվում են նրա գործակիցներ։ Այս դեպքում a գործակիցը ընդունված է անվանել ավագ, իսկ c գործակիցը՝ ազատ։ Յուրաքանչյուր գործակցի փոփոխությունը հանգեցնում է պարաբոլի որոշակի փոխակերպումների։
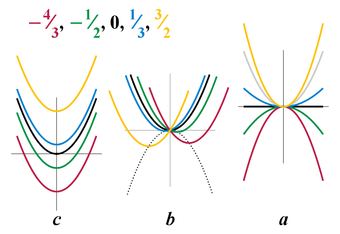
a գործակցի արժեքով կարելի է դատել այն մասին, թե որ ուղղությամբ են ուղղված նրա ճյուղերը (վեր կամ վար) և գնահատել դրա ձգման կամ սեղմման աստիճանը օրդինատների առանցքի նկատմամբ։
Եթե , ապա պարաբոլի ճյուղերը ուղղված են դեպի վեր, այսինքն, նրա գագաթը գտնվում է ներքևում։
Եթե , ապա պարաբոլի ճյուղերը ուղղված են ներքև, այսինքն, նրա գագաթը գտնվում է վերևում։
Եթե , ապա պարաբոլը սեղմվում է օրդինատների առանցքի վրա, այսինքն, կարծես ավելիկ այն է և հարթ։
Եթե , ապա պարաբոլը ձգվել է օրդինատների առանցքի վրա, այսինքն, կարծես ավելի նեղ է և կտրուկ։
a գործակցի արժեքի ազդեցությունը առավել պարզապես թույլ է տալիս ցույց պատկերացնել ֆունկցիայի տեսքը կախված գործակցի արժեքից, այսինքն, այն դեպքում, երբ b=0 և C=0, ապա։ Այն դեպքում, երբ քառակուսի ֆունկցիան վերածվում է գծայինի։
c գործակիցը բնութագրում է պարաբոլայի զուգահեռ տեղափոխությունը օրդինատների առանցքի նկատմամբ (այսինքն՝ վեր կամ վար)։ Այս գործակցի արժեքը 1-ով բարձրացնելու դեպքում գրաֆիկը տեղափոխում է 1-ով։ Համապատասխանաբար, եթե դուք նվազեցնել գործակիցը պարաբոլը կտեղափոխվի ներքև։ Քանի որ, գործակիցը նույնպես ազդում է պարաբոլայի վերին դիրքի վրա, ապա միայն c գործակցի արժեքից չի կարելի դատել այն մասին, թե արդյոք գագաթը գտնվում է աբսցիսների առանցքից բարձր կամ ցածր։

Ցանկացած տեսքի քառակուսային ֆունկցիայի ձևափոխումը տեսքի, թույլ է տալիս օգտվել երկանդամների կրճատ բազմապատկման բանաձևերից։
-
- , где и
Ֆունկցիայի զրոներ
[խմբագրել | խմբագրել կոդը]
Քառակուսային ֆունկցիան երկրորդ աստիճանի ամբողջ ռացիոնալ ֆունկցիա է, ուստի այն կարող է ունենալ ոչ ավելի, քան երկու զրոներ իրական տիրույթում։
Առանց համապատասխան քառակուսի հավասարման լուծման, քառակուսային ֆունկցիայի զրոները որոշելը հնարավոր է դիսկրիմինանտի հաշվման միջոցով։
| Լրիվ դիսկրիմինանտ (որոշիչ) | Կրճատ դիսկրիմինանտ | Բերված դիսկրիմինանտ |
|---|---|---|
Անկախ դիսկրիմինանտի որոշմանձևից ճիշտ են հետևյալ պնդումները․
- Եթե , ապա պարաբոլի գագաթի աբսցիսը կլինի ֆունկցիայի միակ զրոն։
- Եթե , ապա ֆունկցիան ունի աբսցիսների առանցքի հետ երկու հատման կետ,այսինքն երկու զրո։
- Եթե , ապա ֆունկցիան զրոներ չունի, քանի որ գրաֆիկը չի հատվում աբսցիսների առանցքի հետ։
- Օրինակ, ֆունկցիայի համար՝
- .
Սա նշանակում է,որ տվյալ ֆունկցիան ունի երկու իրական զրոներ։
Դրսևորումներ գործնականում
[խմբագրել | խմբագրել կոդը]
- Ազատ անկում կատարող մարմնի բարձրության կախումը ժամանակից․
- Շրջանի չափերի կախումը իր գծային չափերից օրինակ՝ շառավղից։
- Հավասարաչափ փոփոխական շարժման տեղափոխության կախումը ժամանակից։
Տես նաև
[խմբագրել | խմբագրել կոդը]- Քառակուսային եռանդամ
- Պարաբոլ
Ծանոթագրություն
[խմբագրել | խմբագրել կոդը]- ↑ Квадратичная функция // Большая школьная энциклопедия. — М. : «Русское энциклопедическое товарищество», 2004. — С. 118—119.
Գրականություն
[խմբագրել | խմբագրել կոդը]- Сканави М.И. График квадратного трёхчлена // Элементарная математика. — 2-е изд., перераб. и доп. — М., 1974. — С. 130—133. — 592 с.
- Каплан И.А. Тридцать третье практическое занятие (экстремум квадратичной функции) // Практические занятия по высшей математике. — 3-е изд. — Харьков, 1974. — С. 449—451.










![{\displaystyle E(f)=\left(-\infty ;-{\frac {b^{2}-4ac}{4a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80574007c87fd2e0a084cba4db58f5eaa2f68950)











![{\displaystyle \left(-\infty ;-{\frac {b}{2a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6b6c026c5999b70af07f10b99f04c9f3eb4cc4)